Das Stellenwertverständnis und die digitale Stellenwerttafel

Unsere heutige Zahlschrift ist äußerst elegant und effizient. Sie ist das Endprodukt eines jahrtausendealten Entwicklungsprozesses. Mit lediglich zehn Zahlsymbolen können wir leicht beliebig große und kleine Zahlen aufschreiben, und auch sehr einfach mit ihnen rechnen. In der römischen Zahlschrift ist das bekanntlich nicht der Fall. Die Genialität unseres Zahlensystems spiegelt sich darin wider, dass den Ziffern kein fester Zahlwert zugeordnet ist, sondern dass der Wert je nach Position innerhalb der Zahl unterscheidet. Unser Stellenwertsystem lässt sich mit vier Prinzipien charakterisieren (vgl. Ross 1989):
Stellenwertprinzip: Die Position einer Ziffer bestimmt ihren Wert.
Bündelungsprinzip: Der Wert jeder Stelle/Bündelungseinheit steigt um den Faktor 10 von rechts nach links.
Multiplikatives Prinzip: Da jede Ziffer die Anzahl der Elemente einer Bündelungseinheit angibt, ergibt sich ihr Zahlenwert aus Ziffer multipliziert mit ihrem Stellenwert.
Additives Prinzip: Der Gesamtwert der Zahl ist die Summe der Zahlenwerte aller Ziffern.

Neben der Einsicht in diese vier Prinzipien, sollten die Schülerinnen und Schüler in der Lage sein, flexibel mit Zahldarstellungen umgehen zu können. Das heißt, sie können schnell und sicher verschiedene Teilungsdarstellungen einer Zahl finden und zwischen ihnen wechseln. Die Zahl 23 lässt sich beispielsweise als 2Z 3E (Standard-Teilung), 1Z 13E oder 23E (nicht-Standard-Teilungen) darstellen. Einheiten von Stellenwerten (ent-)bündeln zu können, ist Grundvoraussetzung für flexible Arithmetik und damit auch für den sicheren Umgang mit allen Grundrechenoperationen. Nicht-Standard-Teilungen sind den Schülerinnen und Schülern zum Beispiel aus Jahreszahlangaben bekannt („neunzehnhundertneunzig“).

Umsetzung im Unterricht

Im Unterricht können Bündelungshandlungen und ein flexibles Stellenwertverständnis mit der Stellenwerttafel erarbeitet und geübt werden. Padberg & Benz (2011) empfehlen den Einsatz der Stellenwerttafel im Unterricht der Grundschule zur Verständnisförderung des Aufbaus und der Struktur des dezimalen Stellenwertsystems sowie zur Verdeutlichung des Zusammenhangs zwischen den einzelnen Stellenwerten.

In einer Stellenwerttafel werden Zahlen repräsentiert, indem Plättchen als Einheiten in Spalten gelegt werden, die für Stellenwerte stehen. Die Tätigkeit des Verschiebens eines Plättchens von einer zur anderen Spalte hat innerhalb der herkömmlichen Stellenwerttafel eine Änderung des Zahlenwertes zur Folge (siehe Abbildung 1), da die Anzahl der verwendeten Plättchen gleich bleibt.

     
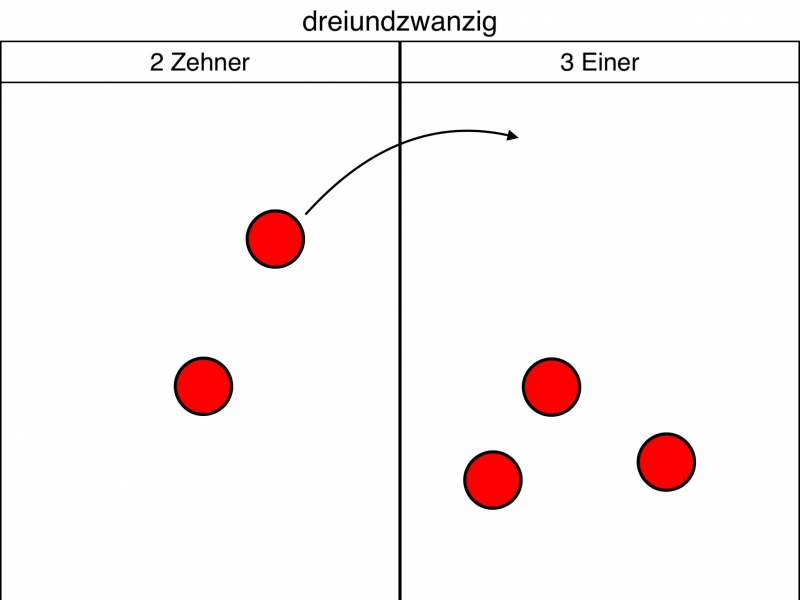
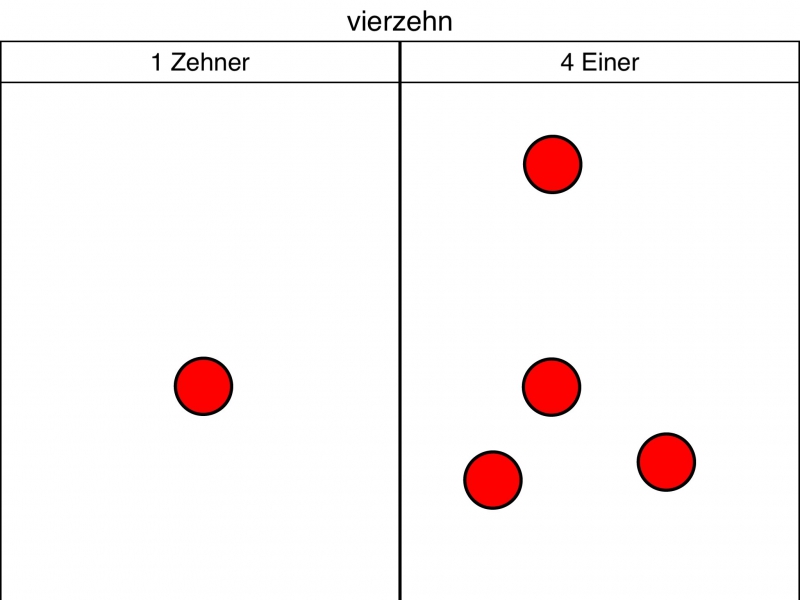
Abb. 1: Zahlwertveränderung

Um zwischen verschiedenen Teilungs-Darstellungen einer Zahl (Standard und nicht-Standard) zu wechseln, muss eigenständig eine entsprechende Anzahl von Plättchen in Spalten hinzugefügt oder aus ihnen entfernt werden. Dies erfordert ein Verständnis des Bündelungsprinzips und es besteht die Gefahr, dass Fehler beim Bündeln passieren und sich damit der Zahlenwert ungewollt ändert. Im Gegensatz dazu bleibt bei der digitalen Stellenwerttafel der Zahlenwert invariant, wenn ein Plättchen in eine andere Spalte bewegt wird (siehe Abbildung 2). 

     
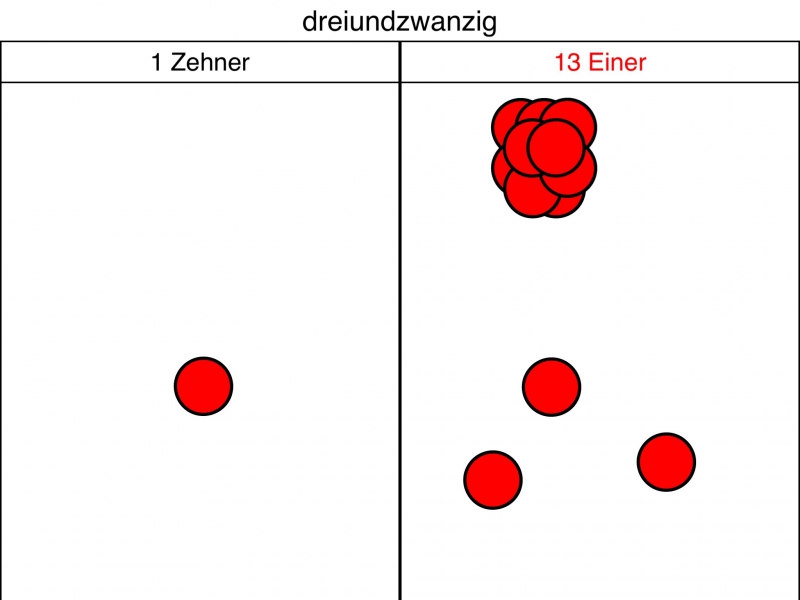
Abb. 2: invarianter Zahlwert

In der Reaktion der Stellenwert-App auf das Verschieben von Plättchen sind die Regeln des Stellenwertsystems kodiert (vgl. Ladel & Kortenkamp 2013). 

Neben diesen zentralen Eigenschaften verfügt die Stellenwert-App über verschiedene zusätzliche Funktionen und gestalterische Feinheiten, die das Stellenwertverständnis fördern sollen: Der Zahlenwert kann als Dezimalzahl oder als Zahlwort ein- und ausgeblendet werden. In jeder Spalte wird die Anzahl der Plättchen automatisch gezählt und im Spaltenkopf vor der Stellenwertbezeichnung als Zahl angezeigt. Sind zehn oder mehr Plättchen in einer Spalte, so signalisiert die rote Farbe, dass umgebündelt werden muss, um zur Standard-Teilung zu gelangen. Die Stellenanzahl kann zwischen zwei bis vier variiert werden. Mit dem Montessori-Modus werden die Plättchen in unterschiedlichen Farben dargestellt. Außerdem kann die Basis zwischen 2 und 16 variiert werden, was ein Arbeiten mit anderen Stellenwertsystemen ermöglicht. In einer weiteren Option kann diese Basis auch der Zählung in den Spaltenköpfen und dem über der Tabelle angezeigten Gesamtwert zugrunde gelegt werden.

Der Übergang von den natürlichen zu den rationalen Zahlen kann verständnisstiftend durch eine Erweiterung der Stellenwerttafel nach rechts erfolgen. Damit soll den Schülerinnen und Schülern veranschaulicht werden, dass die Grundregeln des Stellenwertsystems auch weiterhin gelten – so wie sie sie bereits von den natürlichen Zahlen her kennen.

Der Einsatz der Stellenwerttafel ist nach dem Rahmenlehrplan des Fachs Mathematik für die Grundschule im Land Brandenburg (2004) für alle Jahrgangsstufen vorgesehen. Durch einen „kreativen Umgang“ mit der Stellenwerttafel soll das Stellenwert- und das Bündelungsprinzip vertieft werden.